Закон распределения случайной величины i рассматривался в предыдущем
параграфе.



Для i = 1,2,...,n получаем систему из n независимых случайных величин i,
имеющих одинаковые законы распределения. Если теперь сравнить законы
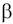
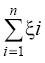
распределения двух случайных величин и , то можно сделать очевидный
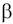
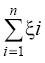
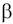
вывод: = . Отсюда следует, что для случайной величины , имеющей
закон распределения Бернулли, математическое ожидание и дисперсия
определяются формулами



Найдём оценку величины р — вероятности успеха в одном испытании
некоторого биномиального эксперимента. Для этого проведём n испытаний и
подсчитаем х – число успехов. Оценку р* неизвестной величины р определим
формулой .
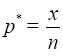