Распределение X2

Пусть имеется n независимых случайных величин 1, 2, ..., n,
распределенных по нормальному закону с математическим ожиданием,
равным нулю, и дисперсией, равной единице. Тогда случайная величина
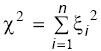
распределена по закону, который называется “распределение
X²” или “распределение Пирсона”. Очевидно, что она может принимать
лишь неотрицательные значения. Число n называется числом степеней
свободы.



При n > 1 график плотности распределения
случайной величины X² представляет собой
кривую, изображенную на рисунке 1.
Для того, чтобы определить вероятность
попадания случайной величины X² в какой-либо
промежуток из множества положительных чисел, пользуются таблицей
распределения X². Обычно такая таблица позволяет



по вероятности q и по числу степеней свободы n определить так
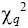
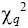
называемый квантиль , если q и связаны соотношением



Эта формула означает: вероятность того, что случайная величина X²
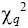
примет значение, большее чем определенное значение , равна q.
Таблица 1 представляет собой фрагмент таблицы распределения X².
Из него видно, что случайная величина X² с 10-ю степенями свободы с
вероятностью q = 0,95 принимает значение, большее 3,94, а та же величина
с одной степенью свободы с вероятностью q = 0,975 превышает 0,00098.