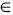
Пусть заданы числа n N и p (0 p 1). Тогда каждому целому числу из
промежутка [0; n] можно поставить в соответствие вероятность, рассчитанную
по формуле Бернулли. Получим закон распределения случайной величины
(назовём её )



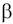
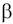
Будем говорить, что случайная величина распределена по закону Бернулли.
Такой случайной величиной является частота появления события А в n
повторных независимых испытаниях, если в каждом испытании событие А
происходит с вероятностью p.
Рассмотрим отдельное i-е испытание. Пространство элементарных
исходов для него имеет вид



Определим на этом пространстве случайную величину i следующим образом: